星语课程网
【阅读记录-章节4】从零构建大语言模型
来源:本站编辑
2025-02-05 14:36
32
4\. Implementing a GPT model from [scratch](https://so.csdn.net/so/search?q=scratch&spm=1001.2101.3001.7020) to generate text ----------------------------------------------------------------------------------------------------------------------------- 在之前的章节中我们已经学习并编码了**多头注意力机制**,这是大型语言模型(LLM)中的核心组件之一。现在,我们将编码LLM的其他构建模块,并将它们组装成一个类似GPT的模型,我们将在下一章训练该模型以生成类人文本。  图4.1中提到的LLM架构包含多个构建模块。在深入介绍各个组件之前,我们将先从整体的模型架构入手进行概述。 ### 4.1 Coding an LLM architecture LLM(Large Language Models,大规模语言模型),如GPT(Generative Pretrained Transformer,生成式预训练变换器),是一种旨在逐字(或逐个标记)生成新文本的深度神经网络架构。尽管这些模型体积庞大,但其架构相对简单,因为许多组件是重复使用的。 GPT类的LLM通常由多个重复的Transformer块组成。以下是GPT模型的主要组成部分: * **输入标记化与嵌入(Tokenization and Embedding):** 将输入的文本转化为模型可以理解的数值表示。 * **多头注意力机制(Masked Multi-Head Attention):** 允许模型在生成下一个词时关注输入序列中的不同部分。 * **Transformer Blocks:** 这些是GPT的核心结构,包含多头注意力机制和前馈神经网络,用于处理和生成文本。  图4.2展示了GPT类LLM的自顶向下视图,突出显示了其主要组件。 在深度学习和LLM中,**“参数”** 指的是模型的可训练权重。这些权重是模型内部的变量,在训练过程中不断调整和优化,以最小化特定的损失函数,从而使模型能够从训练数据中学习。 > **GPT-2与GPT-3的比较** > 目前,我们主要关注GPT-2模型,原因如下: > > * **公开可用的权重:** OpenAI已经公开了GPT-2的预训练权重,可以在第6章中加载到我们的实现中。 > * **模型规模:** GPT-2最小版本有1.24亿个参数,而GPT-3则大幅增加到1750亿个参数,并且训练所使用的数据更多。 > * **资源需求:** GPT-2适合在单台笔记本电脑上运行,而GPT-3需要GPU集群进行训练和推理。例如,据Lambda Labs的数据,使用单个V100数据中心GPU训练GPT-3需要355年,使用消费者级RTX 8000 GPU则需要665年。 > > 由于GPT-3的权重尚未公开,且其训练和使用资源需求极高,GPT-2是学习和实现LLM的更好选择。 #### 4.1.1 配置小型 GPT-2 模型 在前面的章节中,我们已经介绍了LLM架构的几个方面,如输入标记化与嵌入、多头注意力机制等。接下来,我们将实现小型GPT-2模型的核心结构,包括其Transformer块,并训练它生成类似人类的文本。我们通过以下 Python 字典来指定小型 GPT-2 模型的配置,这将在后续的代码示例中使用: GPT_CONFIG_124M = { "vocab_size": 50257, # 词汇表大小 "context_length": 1024, # 上下文长度 "emb_dim": 768, # 嵌入维度 "n_heads": 12, # 注意力头数量 "n_layers": 12, # 层数 "drop_rate": 0.1, # Dropout 比率 "qkv_bias": False # 查询-键-值偏置 } > 在 `GPT_CONFIG_124M` 字典中,我们使用简洁的变量名称以提高代码的可读性,并防止代码行过长: > > * **vocab\_size**:词汇表大小为50,257个词,这是BPE(Byte Pair Encoding)分词器使用的词汇量(详见第2章)。 > * **context\_length**:模型通过位置嵌入(positional embeddings)处理的最大输入标记数(详见第2章)。 > * **emb\_dim**:嵌入维度,表示将每个标记转换为768维的向量。 > * **n\_heads**:多头注意力机制中的注意力头数量(详见第3章)。 > * **n\_layers**:模型中的变换器块(Transformer Blocks)数量,我们将在后续讨论中详细介绍。 > * **drop\_rate**:Dropout机制的强度(0.1表示有10%的隐藏单元会被随机丢弃),用于防止过拟合(详见第3章)。 > * **qkv\_bias**:决定是否在多头注意力机制的线性层中包含查询(Query)、键(Key)和值(Value)的偏置向量。我们将初始设为 `False`,遵循现代LLM的规范,但在第6章加载OpenAI的预训练GPT-2权重时会重新考虑这一点。 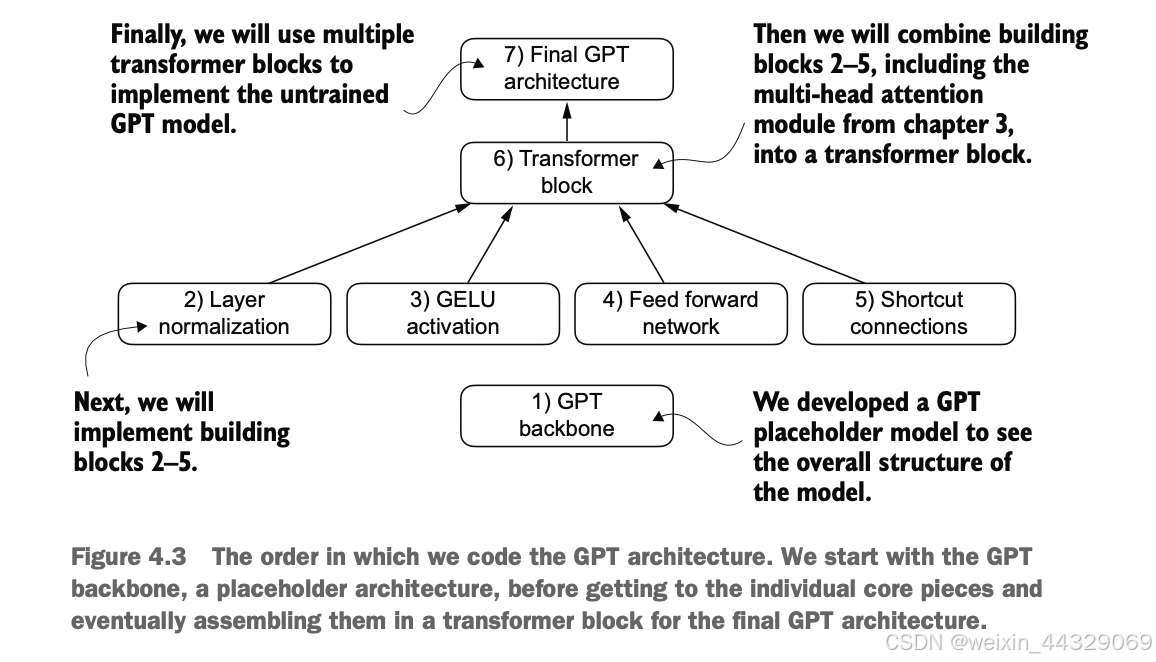 使用上述配置,我们将实现一个DummyGPTModel,如图4.3所示。这将为我们提供一个整体视图,了解各个组件如何协同工作以及组装完整GPT模型架构所需的其他组件。 #### 4.1.2 DummyGPTModel代码示例 import torch import torch.nn as nn # 定义一个DummyGPTModel类 class DummyGPTModel(nn.Module): def __init__(self, cfg): super().__init__() # 标记嵌入层:将输入的标记索引转换为嵌入向量 self.tok_emb = nn.Embedding(cfg["vocab_size"], cfg["emb_dim"]) # 位置嵌入层:为每个标记添加位置信息 self.pos_emb = nn.Embedding(cfg["context_length"], cfg["emb_dim"]) # Dropout层:在训练过程中随机丢弃一部分神经元,防止过拟合 self.drop_emb = nn.Dropout(cfg["drop_rate"]) # Transformer块序列:由多个变换器块(占位符)组成 self.trf_blocks = nn.Sequential( *[DummyTransformerBlock(cfg) for _ in range(cfg["n_layers"])] ) # 最终的层归一化:对输出进行归一化处理 self.final_norm = DummyLayerNorm(cfg["emb_dim"]) # 输出线性层:将嵌入维度转换回词汇表大小,生成logits self.out_head = nn.Linear(cfg["emb_dim"], cfg["vocab_size"], bias=False) def forward(self, in_idx): # 获取批次大小和序列长度 batch_size, seq_len = in_idx.shape # 通过标记嵌入层将输入索引转换为嵌入向量 tok_embeds = self.tok_emb(in_idx) # 生成位置索引并通过位置嵌入层转换为嵌入向量 pos_embeds = self.pos_emb(torch.arange(seq_len, device=in_idx.device)) # 将标记嵌入和位置嵌入相加,得到输入的最终嵌入表示 x = tok_embeds + pos_embeds # 应用Dropout层,随机丢弃部分神经元 x = self.drop_emb(x) # 通过一系列Transformer块进行处理 x = self.trf_blocks(x) # 应用层归一化 x = self.final_norm(x) # 通过输出线性层生成logits logits = self.out_head(x) return logits # 使用占位符替代 TransformerBlock 和 LayerNorm class DummyTransformerBlock(nn.Module): def __init__(self, cfg): super().__init__() # 这里可以添加实际的Transformer块的组件,例如多头注意力机制和前馈神经网络 pass def forward(self, x): # 当前占位符不执行任何操作,直接返回输入 return x class DummyLayerNorm(nn.Module): def __init__(self, normalized_shape, eps=1e-5): super().__init__() # 这里可以添加实际的LayerNorm的参数,例如可学习的缩放因子和偏置 pass def forward(self, x): # 当前占位符不执行任何操作,直接返回输入 return x #### 4.1.3 准备输入数据并初始化 GPT 模型 接下来,我们将准备输入数据并初始化一个新的GPT模型,以展示其用法。在前面的章节中,我们已经介绍了分词器(详见第2章),以下是一个简单的分词器示例: import tiktoken import torch # 获取GPT-2的分词器 tokenizer = tiktoken.get_encoding("gpt2") # 创建一个批次,包括两个文本输入 batch = [] txt1 = "Every effort moves you" txt2 = "Every day holds a" batch.append(torch.tensor(tokenizer.encode(txt1))) batch.append(torch.tensor(tokenizer.encode(txt2))) # 将批次堆叠成一个张量 batch = torch.stack(batch, dim=0) print(batch) **输出示例:** tensor([[6109, 3626, 6100, 345], [6109, 1110, 6622, 257]]) * 第一行对应第一个文本 `"Every effort moves you"` 的标记ID。 * 第二行对应第二个文本 `"Every day holds a"` 的标记ID。 现在让我们看看**数据如何在GPT模型中流动**,如图4.4所示。 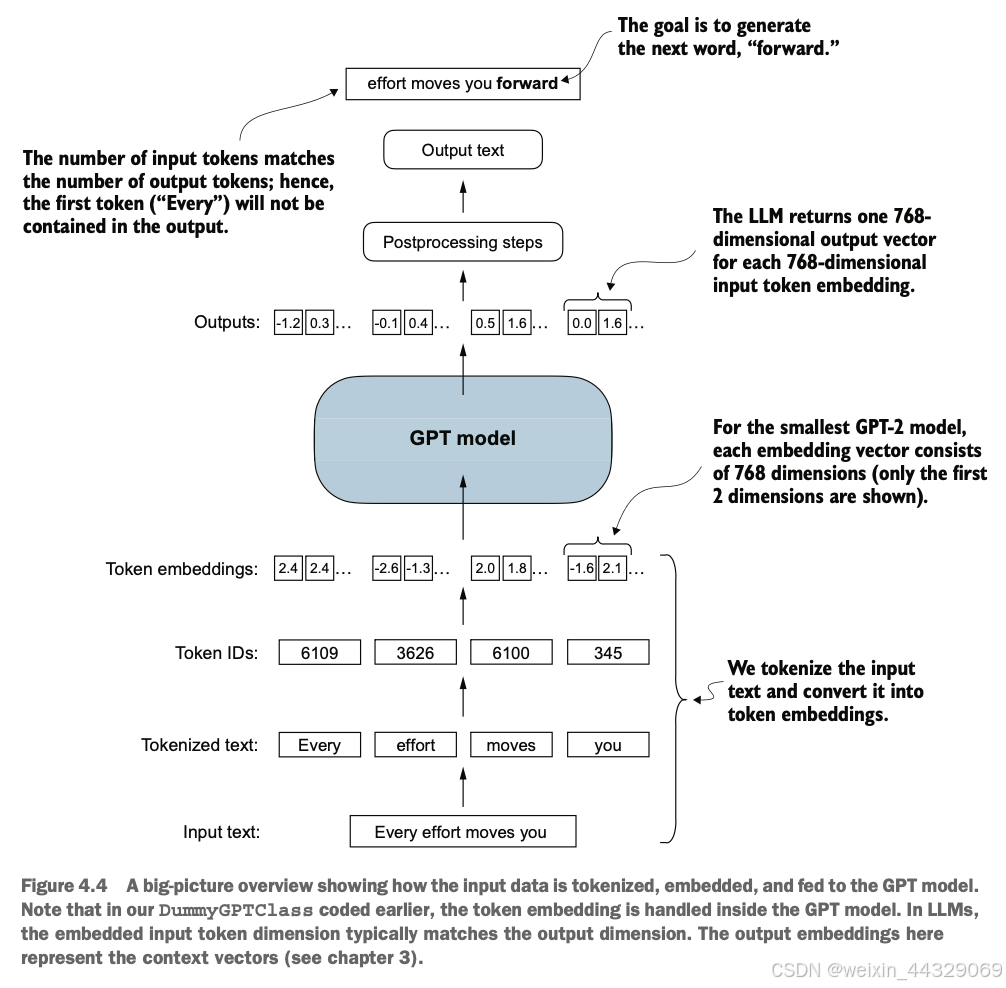 #### 4.1.4 初始化并运行 GPT 模型 # 设置随机种子以确保结果可重复 torch.manual_seed(123) # 初始化 DummyGPTModel 实例 model = DummyGPTModel(GPT_CONFIG_124M) # 将标记化的批次输入模型 logits = model(batch) # 打印输出形状和内容 print("Output shape:", logits.shape) print(logits) **输出示例:** Output shape: torch.Size([2, 4, 50257]) tensor([[[-1.2034, 0.3201, -0.7130, ..., -1.5548, -0.2390, -0.4667], [-0.1192, 0.4539, -0.4432, ..., 0.2392, 1.3469, 0.5307], [ 1.6720, -0.4695, 1.1966, ..., 0.0111, 0.0139, 1.6755], [-0.3388, 1.1586, -1.0908, ..., -1.6047, -0.7860, 0.5581]], [[-0.0610, 0.4835, -0.0077, ..., 0.3567, 1.2698, -0.6398], [-0.0162, -0.1296, -0.2407, ..., 2.0057, -0.3694, 0.1814], [ 0.5835, -0.0435, -1.0400, ..., 0.2439, -0.4530, 1.6621], [ 0.3717, ...]]]) > **解释:** > > * **输出形状**:`torch.Size([2, 4, 50257])` > * **2**:批次大小,对应两个文本样本。 > * **4**:每个文本样本的标记数。 > * **50257**:每个标记对应的词汇表大小维度。 > * **logits**:模型的输出,被称为logits。每个logit是一个50,257维的向量,对应词汇表中每个词的得分。稍后在后处理步骤中,我们将这些向量转换回标记ID,再解码成实际的词语。 通过以上步骤,我们: 1. **配置了小型GPT-2模型**,定义了模型的各项参数。 2. **实现了一个占位的GPT模型架构(DummyGPTModel)**,包括标记嵌入、位置嵌入、Dropout、多层变换器块、层归一化和线性输出层。 3. **准备了输入数据**,使用GPT-2的分词器将文本转换为标记ID。 4. **初始化并运行了GPT模型**,获得了模型的输出logits。 目前,`DummyGPTModel` 中的 `DummyTransformerBlock` 和 `DummyLayerNorm` 只是占位符,未来将被实际的Transformer块和层归一化类替代。在接下来的章节中,我们将逐步实现这些组件,并加载预训练的GPT-2权重,以构建一个功能完整的GPT模型。 ### 4.2 Normalizing activations with layer normalization **训练**具有**多层**的深度神经网络有时会面临诸如**梯度消失(vanishing gradients)** 或 **梯度爆炸(exploding gradients)** 的问题。这些问题会导致训练动态不稳定,使网络难以有效调整其权重,从而导致学习过程难以找到一组能够最小化损失函数的参数(权重)。换句话说,**网络难以学习数据中的潜在模式,无法做出准确的预测或决策**。 > **注意**:如果您对神经网络训练和梯度概念不熟悉,可以参考附录A中的A.4节进行简要介绍。然而,理解梯度的深层数学原理并不是理解本书内容的必要条件。 为了改善神经网络训练的稳定性和效率,我们现在实现层归一化。**层归一化**的主要思想是**调整神经网络层的激活(输出)使其均值为0,方差为1(即单位方差)**。这种调整加速了收敛速度,并确保训练过程的一致性和可靠性。在GPT-2和现代的变换器架构中,层归一化通常在多头注意力模块的前后以及最终输出层之前应用,如我们在`DummyLayerNorm` 中所见。图4.5 展示了层归一化的工作原理。 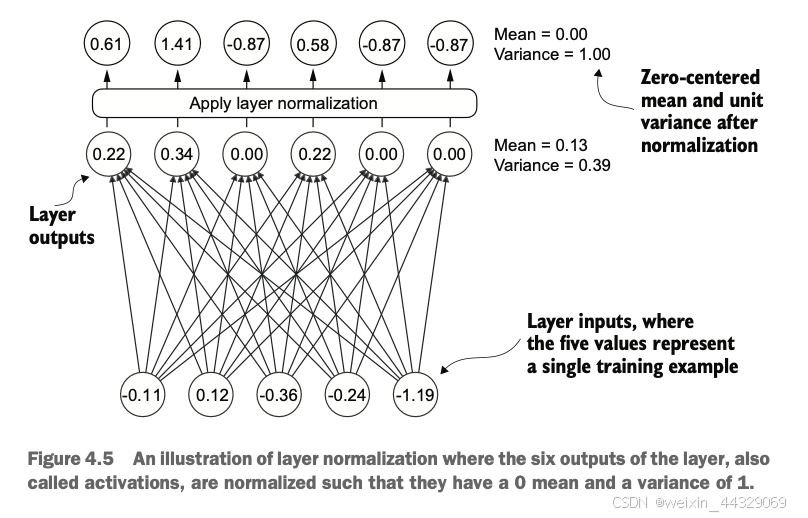 我们可以通过以下代码重新创建图4.5中展示的示例,其中我们实现了一个具有五个输入和六个输出的神经网络层,并将其应用于两个输入示例: import torch import torch.nn as nn # 设置随机种子以确保结果可重复 torch.manual_seed(123) # 创建两个训练示例,每个示例有五个维度(特征) batch_example = torch.randn(2, 5) # 定义一个简单的神经网络层:线性层后接ReLU激活函数 layer = nn.Sequential(nn.Linear(5, 6), nn.ReLU()) # 将示例输入通过神经网络层 out = layer(batch_example) # 打印输出 print(out) **输出示例**: tensor([[0.2260, 0.3470, 0.0000, 0.2216, 0.0000, 0.0000], [0.2133, 0.2394, 0.0000, 0.5198, 0.3297, 0.0000]], grad_fn=<ReluBackward0>) > **解释**: > 该神经网络层由一个线性层(`Linear`)和一个非线性激活函数ReLU(Rectified Linear Unit)组成。ReLU是一种标准的激活函数,将负值阈值化为0,确保层的输出仅包含正值,这解释了为什么输出中不含负值。 在将层归一化应用于这些输出之前,我们先检查输出的均值和方差: # 计算均值 mean = out.mean(dim=-1, keepdim=True) # 计算方差 var = out.var(dim=-1, keepdim=True) # 打印均值和方差 print("Mean:\n", mean) print("Variance:\n", var) **输出**: Mean: tensor([[0.1324], [0.2170]], grad_fn=<MeanBackward1>) Variance: tensor([[0.0231], [0.0398]], grad_fn=<VarBackward0>) > **解释**: > > * **均值(Mean)**:第一行包含第一个输入行的均值,第二行包含第二个输入行的均值。 > * **方差(Variance)**:第一行包含第一个输入行的方差,第二行包含第二个输入行的方差。 > * 使用 `keepdim=True` 可以确保输出张量保留与输入张量相同的维度数,即使操作会沿着指定的维度(`dim`)减少张量的维度。例如,没有 `keepdim=True`,返回的均值张量将是一个二维向量 `[0.1324, 0.2170]`,而不是一个 2 × 1 维的矩阵 `[[0.1324], [0.2170]]`。  接下来,我们将层归一化应用于之前得到的层输出。该操作包括减去均值并除以方差的平方根(即标准差): # 应用层归一化 out_norm = (out - mean) / torch.sqrt(var) # 重新计算归一化后的均值和方差 mean = out_norm.mean(dim=-1, keepdim=True) var = out_norm.var(dim=-1, keepdim=True) # 打印归一化后的输出、均值和方差 print("Normalized layer outputs:\n", out_norm) print("Mean:\n", mean) print("Variance:\n", var) **输出**: Normalized layer outputs: tensor([[ 0.6159, 1.4126, -0.8719, 0.5872, -0.8719, -0.8719], [-0.0189, 0.1121, -1.0876, 1.5173, 0.5647, -1.0876]], grad_fn=<DivBackward0>) Mean: tensor([[-5.9605e-08], [ 1.9868e-08]], grad_fn=<MeanBackward1>) Variance: tensor([[1.], [1.]], grad_fn=<VarBackward0>) > **解释**: > > * **归一化后的层输出(Normalized layer outputs)**:这些输出现在具有均值为0和方差为1的特性。注意,归一化后的输出中可能包含负值。 > * **均值和方差**:归一化后的均值接近0,方差为1。由于计算机表示数值的有限精度,均值不完全为0,但非常接近。 **提高可读性**: 为了提高输出的可读性,可以关闭科学计数法: # 关闭科学计数法 torch.set_printoptions(sci_mode=False) # 再次打印均值和方差 print("Mean:\n", mean) print("Variance:\n", var) **输出**: Mean: tensor([[ 0.0000], [ 0.0000]], grad_fn=<MeanBackward1>) Variance: tensor([[1.], [1.]], grad_fn=<VarBackward0>) 到目前为止,我们已经逐步编码并应用了层归一化过程。现在,让我们将此过程封装在一个PyTorch模块中,以便在GPT模型中使用。 **代码示例:层归一化类** class LayerNorm(nn.Module): def __init__(self, emb_dim): super().__init__() self.eps = 1e-5 # 一个小常数,防止除零 self.scale = nn.Parameter(torch.ones(emb_dim)) # 可学习的缩放因子 self.shift = nn.Parameter(torch.zeros(emb_dim)) # 可学习的偏移量 def forward(self, x): # 计算均值 mean = x.mean(dim=-1, keepdim=True) # 计算方差(使用有偏估计) var = x.var(dim=-1, keepdim=True, unbiased=False) # 归一化 norm_x = (x - mean) / torch.sqrt(var + self.eps) # 缩放和平移 return self.scale * norm_x + self.shift > **解释**: > > * **LayerNorm 类**:该类实现了层归一化操作。 > * **`self.eps`**:一个小常数(epsilon),用于在归一化时防止除以零。 > * **`self.scale` 和 `self.shift`**:可学习的参数,用于缩放和偏移归一化后的输出,使模型能够学习到适合数据的最佳缩放和平移。 > * **前向传播方法(`forward`)**: > * 计算输入张量 `x` 在最后一个维度上的均值和方差。 > * 对输入进行归一化处理。 > * 应用缩放和平移,生成最终输出。 > **有偏方差(Biased Variance)**: > 在方差计算中,我们设置 `unbiased=False`,这意味着在方差公式中使用的是输入数量 `n` 而不是 `n-1`,这不会应用贝塞尔校正(Bessel’s correction)。对于LLMs(大规模语言模型),嵌入维度 `n` 通常很大,使用 `n` 和 `n-1` 的差异可以忽略。因此,这种有偏估计方法确保了与GPT-2模型的归一化层兼容,并反映了最初实现GPT-2模型时使用的TensorFlow默认行为。 现在,让我们实际应用 `LayerNorm` 模块并将其应用于批量输入: # 初始化层归一化模块,嵌入维度为5 ln = LayerNorm(emb_dim=5) # 将层归一化应用于示例输入 out_ln = ln(batch_example) # 重新计算归一化后的均值和方差 mean = out_ln.mean(dim=-1, keepdim=True) var = out_ln.var(dim=-1, unbiased=False, keepdim=True) # 打印归一化后的均值和方差 print("Mean:\n", mean) print("Variance:\n", var) **输出**: Mean: tensor([[-0.0000], [ 0.0000]], grad_fn=<MeanBackward1>) Variance: tensor([[1.0000], [1.0000]], grad_fn=<VarBackward0>) > **解释**: > > * **归一化后的均值**:接近0。 > * **归一化后的方差**:等于1。 > * 这表明层归一化已经成功地规范化了输入,使其具有均值为0和方差为1的特性。 ##### 补充介绍:Layer normalization vs. batch normalization * **批归一化**适用于批次大小较大且固定的场景,通过批次内归一化加速训练。 * **层归一化**更适用于批次大小不固定或较小的场景,特别是在LLMs中因其独立于批次大小的特性,提供了更高的灵活性和稳定性。 **1\. 批归一化(Batch Normalization)** * **定义**:在训练批次内对每个特征维度进行归一化。 * **优点**: * 加速训练过程。 * 提高模型性能。 * **缺点**: * 依赖于批次大小,批次过小时效果不佳。 * 在分布式训练中实现较复杂,因为需要跨设备共享统计量。 **2\. 层归一化(Layer Normalization)** * **定义**:在每个样本的特征维度上进行归一化,不依赖于批次大小。 * **优点**: * **灵活性高**:不受批次大小限制,适用于各种硬件配置和使用场景。 * **稳定性好**:每个样本独立归一化,避免批次内样本间的依赖关系。 * **适合分布式训练**:无需跨设备共享统计量,实现更简单。 * **一致性**:训练和推理阶段行为一致,便于模型部署。 * **缺点**: * 在某些情况下,可能不如批归一化有效,但在LLMs中这一点影响较小。 > **为什么在LLMs中更倾向于使用层归一化** > > * **计算资源需求高**:LLMs如GPT需要大量计算资源,批次大小可能受限。 > * **分布式训练**:层归一化更适合在分布式环境中使用,简化实现。 > * **资源受限环境**:在资源有限的情况下,层归一化依然能保持模型稳定性和性能。  通过本节内容,我们完成了以下任务: 1. **了解了训练深层神经网络时可能遇到的梯度消失和梯度爆炸问题**,并认识到这些问题会导致训练过程不稳定,影响模型学习能力。 2. **学习并实现了层归一化**,了解其作用是规范化神经网络层的激活,使其均值为0,方差为1,从而加速收敛并提高训练稳定性。 3. **通过代码示例演示了层归一化的实现过程**,包括计算均值和方差、归一化操作,以及封装成PyTorch模块。 4. **验证了层归一化的效果**,确保其输出具有预期的均值和方差。 在接下来的章节中,我们将继续构建GPT模型,首先将替换 `DummyLayerNorm` 为实际的 `LayerNorm` 类,并逐步实现其他关键组件,如GELU激活函数。 ### 4.3 Implementing a feed forward network with GELU activations GELU(Gaussian Error Linear Unit,高斯误差线性单元)是深度学习中常用的一种激活函数,特别是在大规模语言模型(LLMs)中。与传统的ReLU(Rectified Linear Unit)相比,GELU具有更平滑的非线性特性,能够提升模型的优化性能。 **GELU的定义**: GELU ( x ) = x ⋅ Φ ( x ) \\text{GELU}(x) = x \\cdot \\Phi(x) GELU(x)\=x⋅Φ(x) 其中, Φ ( x ) \\Phi(x) Φ(x) 是标准高斯分布的累积分布函数。然而,在实际操作中,通常会实现一个计算成本更低的近似方法(原始的GPT-2模型也是使用这种通过曲线拟合发现的近似方法进行训练的):  import torch import torch.nn as nn class GELU(nn.Module): def __init__(self): super().__init__() def forward(self, x): return 0.5 * x * (1 + torch.tanh( torch.sqrt(torch.tensor(2.0 / torch.pi)) * (x + 0.044715 * torch.pow(x, 3)) )) 通过绘制GELU和ReLU激活函数,可以更直观地理解两者的区别: import matplotlib.pyplot as plt # 实例化激活函数 gelu = GELU() relu = nn.ReLU() # 生成输入数据 x = torch.linspace(-3, 3, 100) # 计算激活函数输出 y_gelu = gelu(x) y_relu = relu(x) # 绘制图形 plt.figure(figsize=(8, 3)) for i, (y, label) in enumerate(zip([y_gelu, y_relu], ["GELU", "ReLU"]), 1): plt.subplot(1, 2, i) plt.plot(x, y) plt.title(f"{label} 激活函数") plt.xlabel("x") plt.ylabel(f"{label}(x)") plt.grid(True) plt.tight_layout() plt.show()  > > * **ReLU**:线性分段函数,正值直接输出,负值输出为0。 > * **GELU**:平滑非线性函数,对大多数负值也有小幅输出。 接下来,我们将使用GELU函数来实现一个小型的神经网络模块——FeedForward,这个模块将在后续的大规模语言模型(LLM)的变换器块中使用。 class FeedForward(nn.Module): def __init__(self, cfg): super().__init__() self.layers = nn.Sequential( nn.Linear(cfg["emb_dim"], 4 * cfg["emb_dim"]), # 扩展维度 GELU(), # GELU激活 nn.Linear(4 * cfg["emb_dim"], cfg["emb_dim"]) # 回缩维度 ) def forward(self, x): return self.layers(x) > **解释**: > > * **第一层线性变换**:将嵌入维度从768扩展到3072(4倍)。 > * **GELU激活**:引入非线性。 > * **第二层线性变换**:将维度回缩到原始的768。 正如我们所见,FeedForward 模块是一个由两个线性层和一个 GELU 激活函数组成的小型神经网络。在拥有1.24亿参数的 GPT 模型中,它通过 `GPT_CONFIG_124M` 字典接收输入批次,这些批次中的每个标记的嵌入维度为768,即 `GPT_CONFIG_124M["emb_dim"] = 768`。图4.9展示了当我们传入一些输入时,这个小型前馈神经网络内部如何操作嵌入维度。  # 定义模型配置 GPT_CONFIG_124M = { "emb_dim": 768, # 嵌入维度 # 其他配置参数... } # 初始化前馈网络 ffn = FeedForward(GPT_CONFIG_124M) # 创建示例输入张量,形状为 [批次大小, 令牌数, 嵌入维度] x = torch.rand(2, 3, 768) # 前向传播 out = ffn(x) # 输出形状 print(out.shape) # 输出: torch.Size([2, 3, 768]) > **解释**: > > * **输入张量**:形状为 `[2, 3, 768]`,表示批次大小为2,每个样本有3个令牌,每个令牌的嵌入维度为768。 > * **输出张量**:形状与输入相同,通过前馈网络处理后,嵌入维度保持一致。 前馈网络通过扩展和回缩嵌入维度,允许模型在更高维的空间中进行复杂的特征转换,从而提升模型的表达能力和学习效果。这种设计使得模型能够探索更丰富的表示空间,有助于更好地捕捉数据中的复杂模式。 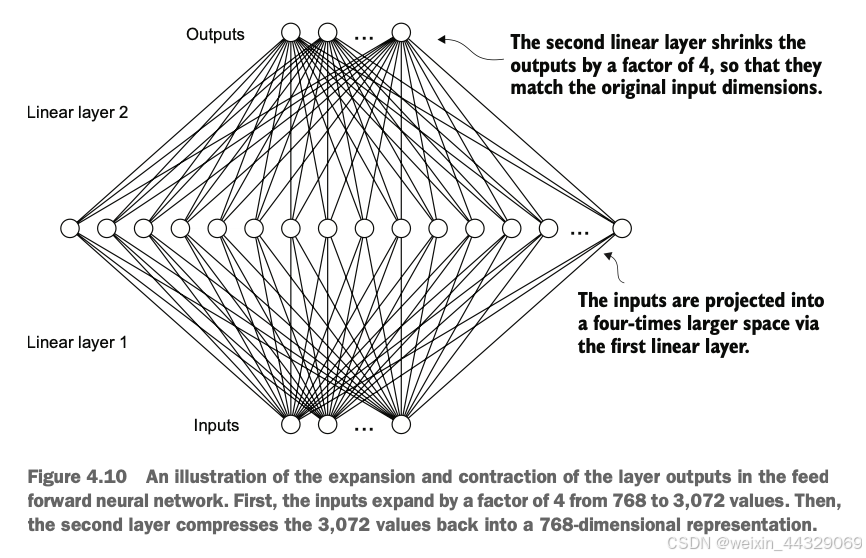 此外,输入和输出维度的一致性简化了架构设计,使得多个层可以堆叠起来(我们稍后会进行此操作),无需在层与层之间调整维度,从而提升了模型的可扩展性。  正如图4.11所示,我们已经实现了大规模语言模型(LLM)的大部分构建模块。接下来,我们将讨论神经网络中插入不同层之间的shortcut connections的概念,这对于改善深度神经网络架构的训练性能至关重要。 ### 4.4 Adding shortcut connections **Shortcut Connections**,也称为**跳跃连接(skip connections)** 或 **残差连接(residual connections)**,最初在计算机视觉中的残差网络(Residual Networks)中提出,目的是缓解深层网络中梯度消失(vanishing gradients)的问题。梯度消失问题指的是在反向传播过程中,梯度(用于指导权重更新)随着层数的增加逐渐变小,导致前面的层难以有效训练,无法很好地学习数据中的模式。  图4.12展示了Shortcut Connections如何为梯度在网络中流动创建一个替代的、更短的路径,方法是跳过一个或多个层。这通过将某一层的输出与后续层的输出相加实现,因此这些连接也被称为跳跃连接(skip connections)。这种设计在训练过程中有助于保持梯度的流动,防止梯度消失,从而提高深层网络的训练性能。 **示例代码:实现带有Shortcut Connections的深层神经网络** 以下代码实现了一个包含五个层的深层神经网络,每个层由一个线性层和一个GELU激活函数组成。网络可以选择是否使用Shortcut Connections: import torch import torch.nn as nn class ExampleDeepNeuralNetwork(nn.Module): def __init__(self, layer_sizes, use_shortcut): super().__init__() self.use_shortcut = use_shortcut self.layers = nn.ModuleList([ nn.Sequential(nn.Linear(layer_sizes[0], layer_sizes[1]), GELU()), nn.Sequential(nn.Linear(layer_sizes[1], layer_sizes[2]), GELU()), nn.Sequential(nn.Linear(layer_sizes[2], layer_sizes[3]), GELU()), nn.Sequential(nn.Linear(layer_sizes[3], layer_sizes[4]), GELU()), nn.Sequential(nn.Linear(layer_sizes[4], layer_sizes[5]), GELU()) ]) def forward(self, x): for layer in self.layers: layer_output = layer(x) if self.use_shortcut and x.shape == layer_output.shape: x = x + layer_output # 添加捷径连接 else: x = layer_output return x # 定义GELU激活函数 class GELU(nn.Module): def __init__(self): super().__init__() def forward(self, x): return 0.5 * x * (1 + torch.tanh( torch.sqrt(torch.tensor(2.0 / torch.pi)) * (x + 0.044715 * torch.pow(x, 3)) )) 首先,我们初始化一个不使用Shortcut Connections的模型,并观察梯度的变化: # 定义层大小 layer_sizes = [3, 3, 3, 3, 3, 1] # 创建示例输入 sample_input = torch.tensor([[1., 0., -1.]]) # 设置随机种子以确保结果可重复 torch.manual_seed(123) # 初始化不使用捷径连接的模型 model_without_shortcut = ExampleDeepNeuralNetwork(layer_sizes, use_shortcut=False) # 定义一个函数来打印梯度 def print_gradients(model, x): output = model(x) target = torch.tensor([[0.]]) loss_fn = nn.MSELoss() loss = loss_fn(output, target) loss.backward() for name, param in model.named_parameters(): if 'weight' in name: print(f"{name} has gradient mean of {param.grad.abs().mean().item()}") # 打印无捷径连接模型的梯度 print_gradients(model_without_shortcut, sample_input) **输出示例**: layers.0.0.weight has gradient mean of 0.00020173587836325169 layers.1.0.weight has gradient mean of 0.0001201116101583466 layers.2.0.weight has gradient mean of 0.0007152041653171182 layers.3.0.weight has gradient mean of 0.001398873864673078 layers.4.0.weight has gradient mean of 0.005049646366387606 > **解释**: > > * 随着层数的增加,梯度值逐渐变小,表现出梯度消失的问题,使得前面的层难以有效训练。 接下来,我们初始化一个使用Shortcut Connections的模型,并观察梯度的变化: # 设置随机种子以确保结果可重复 torch.manual_seed(123) # 初始化使用捷径连接的模型 model_with_shortcut = ExampleDeepNeuralNetwork(layer_sizes, use_shortcut=True) # 打印使用捷径连接模型的梯度 print_gradients(model_with_shortcut, sample_input) **输出示例**: layers.0.0.weight has gradient mean of 0.22169792652130127 layers.1.0.weight has gradient mean of 0.20694105327129364 layers.2.0.weight has gradient mean of 0.32896995544433594 layers.3.0.weight has gradient mean of 0.2665732502937317 layers.4.0.weight has gradient mean of 1.3258541822433472 > **解释**: > > * 使用捷径连接后,梯度值在各层之间保持较为一致,不再逐渐减小,有效缓解了梯度消失的问题。 **总结** * **梯度消失问题**:在深层神经网络中,梯度随着层数的增加而逐渐变小,导致前面的层难以训练。 * **Shortcut Connections的优势**: * **保持梯度流动**:通过创建更短的路径,确保梯度在反向传播过程中不会过度衰减。 * **提升训练性能**:有助于更有效地训练深层网络,提高模型的学习能力。 * **简化架构**:使得堆叠多个层更加容易,提升模型的可扩展性。 在大规模语言模型(LLMs)如GPT-2中,Shortcut Connections是核心构建块之一,确保了模型在训练过程中的稳定性和效率,并支持更深层次的网络架构。 ### 4.5 Connecting attention and linear layers in a transformer block 接下来,我们将实现Transformer块,这是GPT和其他LLM架构中的基本构建模块。在拥有1.24亿参数的GPT-2架构中,这个块重复了十几次。一个Transformer块结合了我们之前介绍的多个概念: * **多头注意力(Multi-Head Attention)** * **层归一化(Layer Normalization)** * **Dropout** * **前馈网络层(Feed Forward Layers)** * **GELU激活函数**  图4.13展示了一个Transformer块,结合了多个组件,包括掩蔽多头注意力模块(详见第3章)和我们之前实现的FeedForward模块(详见第4.3节)。当Transformer块处理输入序列时,序列中的每个元素(例如,一个单词或子词标记)由一个固定大小的向量表示(在此例中为768维)。Transformer块内的操作,包括多头注意力和前馈网络,旨在以保持维度一致的方式转换这些向量。 > **核心思想**: > > * **自注意力机制(Self-Attention Mechanism)**:在多头注意力模块中,识别并分析输入序列中元素之间的关系。 > * **前馈网络(Feed Forward Network)**:在每个位置上单独修改数据。 这种组合不仅允许更细致地理解和处理输入,还增强了模型处理复杂数据模式的整体能力。 **以下是Transformer块在PyTorch中的实现示例:** from chapter03 import MultiHeadAttention # 假设MultiHeadAttention在chapter03中定义 import torch import torch.nn as nn class TransformerBlock(nn.Module): def __init__(self, cfg): super().__init__() # 多头注意力机制 self.att = MultiHeadAttention( d_in=cfg["emb_dim"], d_out=cfg["emb_dim"], context_length=cfg["context_length"], num_heads=cfg["n_heads"], dropout=cfg["drop_rate"], qkv_bias=cfg["qkv_bias"] ) # 前馈网络 self.ff = FeedForward(cfg) # 层归一化 self.norm1 = LayerNorm(cfg["emb_dim"]) self.norm2 = LayerNorm(cfg["emb_dim"]) # Dropout用于正则化 self.drop_shortcut = nn.Dropout(cfg["drop_rate"]) def forward(self, x): # 第一部分:多头注意力 shortcut = x # 保存输入以便后续添加 x = self.norm1(x) # 归一化 x = self.att(x) # 应用多头注意力 x = self.drop_shortcut(x) # Dropout x = x + shortcut # 添加shortcut连接 # 第二部分:前馈网络 shortcut = x # 保存当前输出 x = self.norm2(x) # 归一化 x = self.ff(x) # 应用前馈网络 x = self.drop_shortcut(x) # Dropout x = x + shortcut # 添加shortcut连接 return x > **解释**: > > * **多头注意力机制(MultiHeadAttention)**:处理输入序列中的依赖关系,捕捉不同子空间的信息。 > * **前馈网络(FeedForward)**:进一步处理每个位置上的数据,增强模型的表达能力。 > * **层归一化(LayerNorm)**:在每个主要组件前进行归一化,稳定训练过程。 > * **捷径连接(Shortcut Connections)**:通过将输入添加到输出,帮助梯度在深层网络中顺利传播,缓解梯度消失问题。 > * **Dropout**:防止过拟合,提高模型的泛化能力。 以下示例展示了如何初始化一个Transformer块并将其应用于样本输入: # 定义模型配置 GPT_CONFIG_124M = { "emb_dim": 768, # 嵌入维度 "context_length": 1024, # 上下文长度 "n_heads": 12, # 注意力头数量 "n_layers": 12, # 层数 "drop_rate": 0.1, # Dropout比率 "qkv_bias": False # 查询-键-值偏置 } # 初始化Transformer块 block = TransformerBlock(GPT_CONFIG_124M) # 创建示例输入张量,形状为 [批次大小, 令牌数, 嵌入维度] x = torch.rand(2, 4, 768) # 前向传播 output = block(x) # 打印输入和输出形状 print("Input shape:", x.shape) # 输出: torch.Size([2, 4, 768]) print("Output shape:", output.shape) # 输出: torch.Size([2, 4, 768]) > **解释**: > > * **输入张量**:形状为 `[2, 4, 768]`,表示批次大小为2,每个样本有4个令牌,每个令牌的嵌入维度为768。 > * **输出张量**:形状与输入相同,表明Transformer块在处理过程中保持了输入的维度不变。 Transformer块通过保持输入和输出维度的一致性,简化了模型架构,使得可以轻松堆叠多个Transformer块而无需调整各层之间的维度。这种设计提高了模型的可扩展性,允许构建更深层次的网络,同时保持计算效率和一致性。 此外,Transformer块中的自注意力机制和前馈网络结合,使模型能够捕捉输入序列中的复杂依赖关系和特征表示,从而提升模型在处理自然语言任务时的表现。  通过实现Transformer块,我们现在拥有了构建GPT架构所需的所有基本模块。如图4.14所示,Transformer块结合了层归一化(Layer Normalization)、前馈网络(Feed Forward Network)、GELU激活函数(GELU Activations)和捷径连接(Shortcut Connections)。正如我们最终将看到的,这个Transformer块将成为GPT架构的主要组成部分。 ### 4.6 Coding the GPT model 我们在本章开始时,通过一个名为DummyGPTModel的整体视图介绍了GPT架构。在这个DummyGPTModel的代码实现中,我们展示了GPT模型的输入和输出,但其构建模块仍然是黑盒,使用DummyTransformerBlock和DummyLayerNorm类作为占位符。 现在,我们将替换DummyTransformerBlock和DummyLayerNorm,使用之前编写的真实TransformerBlock和LayerNorm类,组装出一个完整工作的原始1.24亿参数版本的GPT-2。在第5章中,我们将对GPT-2模型进行预训练,在第6章中,我们将加载OpenAI的预训练权重。  在代码中组装GPT-2模型之前,让我们先看一下其整体结构,如图4.15所示,包含了我们迄今为止覆盖的所有概念。正如我们所见,Transformer块在GPT模型架构中被多次重复。在`1.24亿`参数的`GPT-2`模型中,这个块被重复了`12`次,通过`GPT_CONFIG_124M`字典中的`n_layers`项指定。在拥有`15.42亿`参数的最大`GPT-2`模型中,这个`Transformer`块被重复了`48`次。 最终Transformer块的输出经过最后一次层归一化后,进入线性输出层。这个输出层将Transformer的输出映射到高维空间(在本例中为`50,257`维,对应于模型的词汇表大小),用于预测序列中的下一个标记。 以下是GPT模型在PyTorch中的实现示例: import torch import torch.nn as nn class GPTModel(nn.Module): def __init__(self, cfg): super().__init__() # 标记嵌入层:将输入的标记索引转换为嵌入向量 self.tok_emb = nn.Embedding(cfg["vocab_size"], cfg["emb_dim"]) # 位置嵌入层:为每个标记添加位置信息 self.pos_emb = nn.Embedding(cfg["context_length"], cfg["emb_dim"]) # Dropout层:防止过拟合 self.drop_emb = nn.Dropout(cfg["drop_rate"]) # Transformer块序列:根据层数配置重复TransformerBlock self.trf_blocks = nn.Sequential( *[TransformerBlock(cfg) for _ in range(cfg["n_layers"])] ) # 最终层归一化 self.final_norm = LayerNorm(cfg["emb_dim"]) # 输出线性层:将嵌入维度转换回词汇表大小,生成logits self.out_head = nn.Linear(cfg["emb_dim"], cfg["vocab_size"], bias=False) def forward(self, in_idx): batch_size, seq_len = in_idx.shape # 标记嵌入 tok_embeds = self.tok_emb(in_idx) # 位置嵌入 pos_embeds = self.pos_emb(torch.arange(seq_len, device=in_idx.device)) # 合并标记嵌入和位置嵌入 x = tok_embeds + pos_embeds # 应用Dropout x = self.drop_emb(x) # 通过Transformer块序列处理 x = self.trf_blocks(x) # 最终层归一化 x = self.final_norm(x) # 生成logits logits = self.out_head(x) return logits > **解释**: > > * **GPTModel类**:定义了一个完整的GPT模型,包含标记嵌入、位置嵌入、Dropout、多层Transformer块、最终层归一化和线性输出层。 > * **标记嵌入层(tok\_emb)**:将输入的标记索引转换为固定维度的嵌入向量。 > * **位置嵌入层(pos\_emb)**:为每个标记添加位置信息,使模型能够理解序列中的顺序关系。 > * **Dropout层(drop\_emb)**:在嵌入层后应用Dropout,防止过拟合。 > * **Transformer块序列(trf\_blocks)**:由多个TransformerBlock组成,根据配置的层数(n\_layers)重复。 > * **最终层归一化(final\_norm)**:对Transformer块的输出进行归一化,稳定训练过程。 > * **输出线性层(out\_head)**:将归一化后的输出映射到词汇表大小的维度,生成预测的logits。 以下示例展示了如何初始化一个1.24亿参数的GPT模型并将其应用于示例输入: # 定义模型配置 GPT_CONFIG_124M = { "vocab_size": 50257, # 词汇表大小 "context_length": 1024, # 上下文长度 "emb_dim": 768, # 嵌入维度 "n_heads": 12, # 注意力头数量 "n_layers": 12, # 层数 "drop_rate": 0.1, # Dropout比率 "qkv_bias": False # 查询-键-值偏置 } # 设置随机种子以确保结果可重复 torch.manual_seed(123) # 初始化GPT模型 model = GPTModel(GPT_CONFIG_124M) # 创建示例输入批次 batch = torch.tensor([ [6109, 3626, 6100, 345], [6109, 1110, 6622, 257] ]) # 前向传播 out = model(batch) # 打印输入和输出 print("Input batch:\n", batch) print("\nOutput shape:", out.shape) print(out) **输出示例**: Input batch: tensor([[6109, 3626, 6100, 345], [6109, 1110, 6622, 257]]) Output shape: torch.Size([2, 4, 50257]) tensor([[[ 0.3613, 0.4222, -0.0711, ..., 0.3483, 0.4661, -0.2838], [-0.1792, -0.5660, -0.9485, ..., 0.0477, 0.5181, -0.3168], [ 0.7120, 0.0332, 0.1085, ..., 0.1018, -0.4327, -0.2553], [-1.0076, 0.3418, -0.1190, ..., 0.7195, 0.4023, 0.0532]], [[-0.2564, 0.0900, 0.0335, ..., 0.2659, 0.4454, -0.6806], [ 0.1230, 0.3653, -0.2074, ..., 0.7705, 0.2710, 0.2246], [ 1.0558, 1.0318, -0.2800, ..., 0.6936, 0.3205, -0.3178], [-0.1565, 0.3926, 0.3288, ..., 1.2630, -0.1858, 0.0388]]], grad_fn=<UnsafeViewBackward0>) > **解释**: > > * **输入张量**:形状为 `[2, 4]`,表示批次大小为2,每个样本有4个标记。 > * **输出张量**:形状为 `[2, 4, 50257]`,每个标记被映射到词汇表大小的维度,用于预测下一个标记的概率分布。 通过使用 `numel()` 方法,我们可以计算模型中所有参数的总数: # 计算模型的总参数数量 total_params = sum(p.numel() for p in model.parameters()) print(f"Total number of parameters: {total_params:,}") **输出**: Total number of parameters: 163,009,536 > 注意,虽然我们初始化的是1.24亿参数的GPT模型,但实际参数数量为1.63亿,这是因为GPT-2架构中使用了权重绑定(weight tying)技术,即在词嵌入层和输出层共享权重。 权重绑定意味着词嵌入层和输出层共享相同的权重矩阵。这样可以减少模型的参数数量,降低内存需求,同时提升模型性能。 以下代码展示了如何通过权重绑定调整参数数量: print("Token embedding layer shape:", model.tok_emb.weight.shape) print("Output layer shape:", model.out_head.weight.shape) # 移除输出层的参数数量 total_params_gpt2 = ( total_params - sum(p.numel() for p in model.out_head.parameters()) ) print(f"Number of trainable parameters considering weight tying: {total_params_gpt2:,}") **输出**: Token embedding layer shape: torch.Size([50257, 768]) Output layer shape: torch.Size([50257, 768]) Number of trainable parameters considering weight tying: 124,412,160 通过权重绑定,模型的参数数量降至1.24亿,与原始GPT-2模型相匹配。权重绑定不仅减少了内存占用和计算复杂度,还在实际训练中提升了性能。因此,我们在GPTModel实现中使用了独立的词嵌入和输出层,以获得更好的训练效果和模型性能。 计算模型的内存需求,假设每个参数为32位浮点数(4字节): # 计算模型的总大小(以MB为单位) total_size_bytes = total_params * 4 total_size_mb = total_size_bytes / (1024 * 1024) print(f"Total size of the model: {total_size_mb:.2f} MB") **输出**: Total size of the model: 621.83 MB > **解释**: > > * **总参数数量**:1.63亿个参数,每个参数4字节,总大小约为621.83 MB。 > * **权重绑定后的参数数量**:1.24亿个参数,总大小更小,提升了存储和计算效率。 既然我们已经实现了GPTModel架构,并且看到它输出的数值张量的形状为 `[batch_size, num_tokens, vocab_size]`,让我们编写代码将这些输出张量转换为文本。 ### 4.7 Generating text 生成模型(如LLM)逐步生成文本,一个词(或标记)一个词地生成。 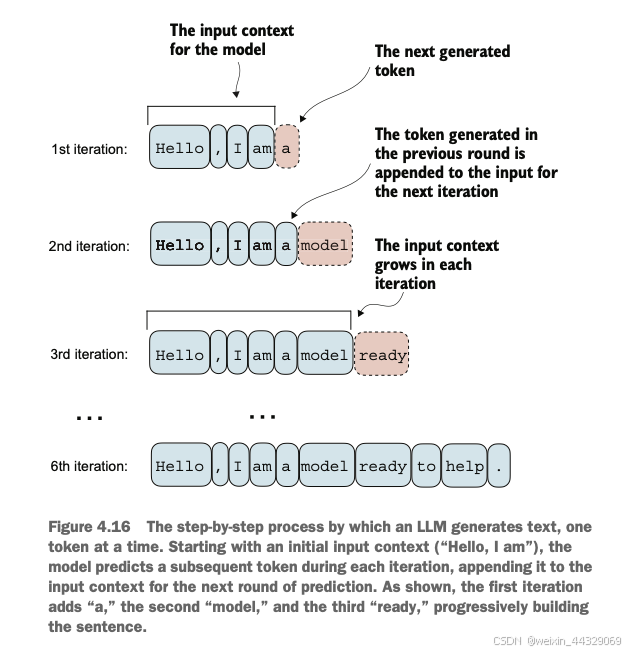 图4.16展示了GPT模型在给定输入上下文(例如,“Hello, I am.”)的情况下,逐步生成文本的过程。每次迭代,输入上下文都会增长,使模型能够生成连贯且上下文相关的文本。到第六次迭代时,模型构建了完整的句子:“Hello, I am a model ready to help.”  GPT模型将输出张量转换为文本涉及多个步骤,如图4.17所示。这些步骤包括解码输出张量、根据概率分布选择标记以及将这些标记转换为人类可读的文本。 > **步骤**: > > 1. **解码输出张量**:将模型输出的logits转换为概率分布。 > 2. **选择下一个标记**:根据概率分布选择下一个标记(通常选择概率最高的标记)。 > 3. **转换为文本**:将选中的标记ID转换回对应的词语或子词标记。 以下是一个简单的生成循环实现,用于从模型输出生成文本: import torch import torch.nn as nn def generate_text_simple(model, idx, max_new_tokens, context_size): for _ in range(max_new_tokens): # 裁剪当前上下文以适应模型的最大上下文长度 # 只保留最后context_size个标记,以确保输入不会超过模型的最大上下文长度 idx_cond = idx[:, -context_size:] # 在推理阶段,我们不需要计算梯度,因此使用torch.no_grad()来节省内存和计算资源 with torch.no_grad(): # 通过模型进行前向传播,得到logits(未归一化的预测分数) logits = model(idx_cond) # 只关注最后一个时间步的logits,因为我们要预测的是序列中的下一个标记 logits = logits[:, -1, :] # logits的形状:[batch_size, vocab_size] # 将logits通过softmax函数转换为概率分布,表示每个标记成为下一个标记的概率 probas = torch.softmax(logits, dim=-1) # 选择概率最高的标记的索引作为下一个标记 # torch.argmax返回最大值的索引,dim=-1表示在词汇表维度上选择 # keepdim=True保持维度不变,便于后续拼接 idx_next = torch.argmax(probas, dim=-1, keepdim=True) # 形状:[batch_size, 1] # 将新生成的标记添加到当前的标记序列中,形成新的输入序列 # torch.cat在第1维(列)上拼接 idx = torch.cat((idx, idx_next), dim=1) # 新的idx形状:[batch_size, n_tokens + 1] # 返回生成的完整标记序列 return idx 接下来我们使用`generate_text_simple`函数生成文本,如图所示,六次迭代的标记预测循环中,模型将一组初始标记ID序列作为输入,预测下一个标记,并将该标记添加到输入序列中以供下一次迭代使用。(标记ID同时被翻译成对应的文本以便更好地理解。) 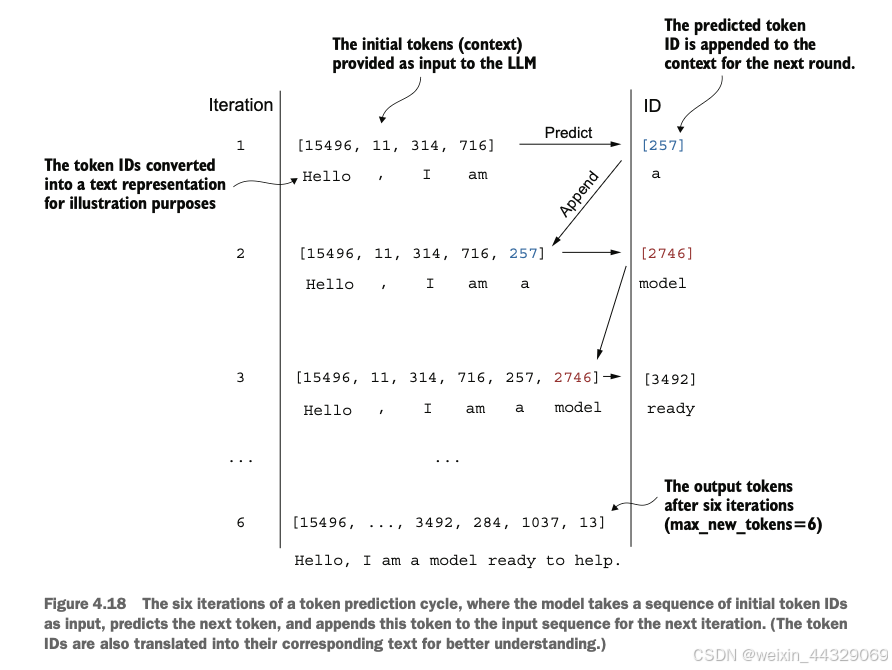 # 假设已经定义并初始化了GPTModel和tokenizer # 编码输入上下文 start_context = "Hello, I am" encoded = tokenizer.encode(start_context) print("encoded:", encoded) encoded_tensor = torch.tensor(encoded).unsqueeze(0) # 形状: [1, 4] print("encoded_tensor.shape:", encoded_tensor.shape) # 将模型设置为评估模式(禁用Dropout) model.eval() # 生成新标记 out = generate_text_simple( model=model, idx=encoded_tensor, max_new_tokens=6, context_size=GPT_CONFIG_124M["context_length"] ) print("Output:", out) print("Output length:", len(out[0])) # 解码生成的标记 decoded_text = tokenizer.decode(out.squeeze(0).tolist()) print(decoded_text) **输出示例**: encoded: [15496, 11, 314, 716] encoded_tensor.shape: torch.Size([1, 4]) Output: tensor([[15496, 11, 314, 716, 27018, 24086, 47843, 30961, 42348, 7267]]) Output length: 10 Hello, I am Featureiman Byeswickattribute argue > **解释**: > > * **输入上下文**:“Hello, I am” 被编码为标记ID `[15496, 11, 314, 716]`。 > * **生成过程**: > * 模型逐步生成6个新标记ID。 > * 最终生成的标记ID序列为 `[15496, 11, 314, 716, 27018, 24086, 47843, 30961, 42348, 7267]`。 > * **解码结果**:“Hello, I am Featureiman Byeswickattribute argue”。 > * 由于模型尚未经过训练,生成的文本是不连贯的。 生成的文本“Hello, I am Featureiman Byeswickattribute argue”是不连贯的,这是因为模型尚未经过训练。到目前为止,我们仅实现了GPT架构并使用随机权重初始化了GPT模型实例。模型训练是一个复杂的过程,我们将在下一章中详细讨论。
点赞
热门评论
最新评论
匿名用户
+1
-1
·
回复TA
暂无热门评论
相关推荐
阅读更多资讯
热门评论 最新评论
暂无热门评论